
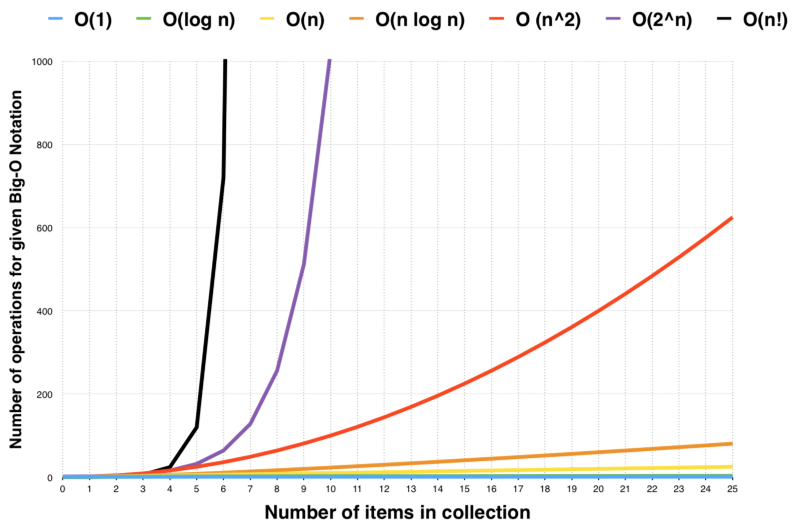
Big-O Algorithm Complexity Cheat Sheet Created Date: 8/24/2016 10:43:56 AM. Time complexity Cheat Sheet. Mac os x for unix. BigO Graph.Correction:- Best time complexity for TIM SORT is O(nlogn). The Azure Machine Learning Algorithm Cheat Sheet helps you choose the right algorithm from the designer for a predictive analytics model. Azure Machine Learning has a large library of algorithms from the classification, recommender systems, clustering, anomaly detection, regression, and text analytics families. The worst-case complexity of an algorithm is the maximum operations algorithm would do for a given input size of n. A big-o notation is a way to represent the growth of a function. In simple words, if I say algorithm run in O(g(n)), then for sufficiently big n, the running time of the algorithm is less than g(n) multiplied by some constant.
- Algorithm Complexity Cheat Sheet Example



Common Data Structure Operations

| Data Structure | Time Complexity | Space Complexity |
|---|
| Average | Worst | Worst |
|---|
| Access | Search | Insertion | Deletion | Access | Search | Insertion | Deletion |
|---|
| Array | Θ(1) | Θ(n) | Θ(n) | Θ(n) | O(1) | O(n) | O(n) | O(n) | O(n) |
| Stack | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Queue | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Singly-Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Doubly-Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Skip List | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n log(n)) |
| Hash Table | N/A | Θ(1) | Θ(1) | Θ(1) | N/A | O(n) | O(n) | O(n) | O(n) |
| Binary Search Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
| Cartesian Tree | N/A | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | N/A | O(n) | O(n) | O(n) | O(n) |
| B-Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Red-Black Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Splay Tree | N/A | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | N/A | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| AVL Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| KD Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
Array Sorting Algorithms
Algorithm Complexity Cheat Sheet Example
| Algorithm | Time Complexity | Space Complexity |
|---|
| Best | Average | Worst | Worst |
|---|
| Quicksort | Ω(n log(n)) | Θ(n log(n)) | O(n^2) | O(log(n)) |
| Mergesort | Ω(n log(n)) | Θ(n log(n)) | O(n log(n)) | O(n) |
| Timsort | Ω(n) | Θ(n log(n)) | O(n log(n)) | O(n) |
| Heapsort | Ω(n log(n)) | Θ(n log(n)) | O(n log(n)) | O(1) |
| Bubble Sort | Ω(n) | Θ(n^2) | O(n^2) | O(1) |
| Insertion Sort | Ω(n) | Θ(n^2) | O(n^2) | O(1) |
| Selection Sort | Ω(n^2) | Θ(n^2) | O(n^2) | O(1) |
| Tree Sort | Ω(n log(n)) | Θ(n log(n)) | O(n^2) | O(n) |
| Shell Sort | Ω(n log(n)) | Θ(n(log(n))^2) | O(n(log(n))^2) | O(1) |
| Bucket Sort | Ω(n+k) | Θ(n+k) | O(n^2) | O(n) |
| Radix Sort | Ω(nk) | Θ(nk) | O(nk) | O(n+k) |
| Counting Sort | Ω(n+k) | Θ(n+k) | O(n+k) | O(k) |
| Cubesort | Ω(n) | Θ(n log(n)) | O(n log(n)) | O(n) |







Comments are closed.